Sextant a jeho použití v praxi
 Sextant je přístroj umožňující měřit úhlové vzdálenosti mezi dvěma body, které jsou od nás tak daleko, že na ně nedosáhneme. Nemůžeme k nim tedy napnout šňůry a změřit úhel mezi těmito šňůrami. Pojmy úhlová vzdálenost a úhel ale chápeme jako synonyma: úhlová vzdálenost je pomyslný úhel mezi dvěma polopřímkami, vedoucími od pozorovatele k jednomu a druhému bodu. Takovým vzdáleným bodem může být například objekt na obloze, horizont na moři nebo i pomyslný bod na obloze přímo nad naší hlavou – zenit.
Sextant je přístroj umožňující měřit úhlové vzdálenosti mezi dvěma body, které jsou od nás tak daleko, že na ně nedosáhneme. Nemůžeme k nim tedy napnout šňůry a změřit úhel mezi těmito šňůrami. Pojmy úhlová vzdálenost a úhel ale chápeme jako synonyma: úhlová vzdálenost je pomyslný úhel mezi dvěma polopřímkami, vedoucími od pozorovatele k jednomu a druhému bodu. Takovým vzdáleným bodem může být například objekt na obloze, horizont na moři nebo i pomyslný bod na obloze přímo nad naší hlavou – zenit.
Nejčastějším použitím sextantu byla v minulosti námořní a letecká navigace. Námořní navigace pomocí sextantu přežila až do dnešních dnů, ale od nástupu GPS ji můžeme považovat spíše za pěkného koníčka nebo jako zálohu pro případ, že selže veškerá elektronika na lodi. Použití sextantu v letectví zažilo největší vzestup během druhé světové války a po ní.
Název sextant pochází z doby, kdy sextanty byly konstruovány jako šestina kruhu. V současnosti ale sextantem nazýváme všechny měřící přístroje založené na stejném principu, bez ohledu na to, jak velkou část kruhu jejich stupnice vytíná.
Rozlišujeme dva typy sextantů: námořní a letecký. Letecký sextant pracuje sice na stejném principu jako námořní, ale zvenku ho vůbec nepřipomíná a vypadá jako krabice ve tvaru mnohoúhelníku. Nebudeme se jím tedy dále zaobírat.
Námořní sextant
Námořní sextant má své uplatnění především v astronavigaci, tedy v navigaci založené na objektech viditelných na obloze. Při námořní astronavigaci měříme úhlovou vzdálenost mezi objektem na obloze a mořským horizontem, hovoříme tedy o tzv. úhlové výšce objektu.
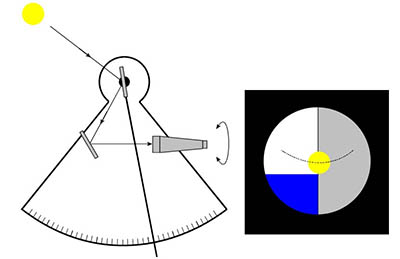
Princip námořního sextantu ukazuje obrázek. Základní částí sextantu je rám tvořící kruhovou výseč se stupnicí na jeho obvodu. Na rámu je připevněno zrcátko Z2 (horizontové zrcátko), jehož rovina je kolmá k rovině rámu, a dalekohled (případně pouze průzor). Zrcátko Z2 sahá pouze do takové vzdálenosti od rámu, aby zabíralo cca polovinu zorného pole dalekohledu. Nahoře je umístěn čep, okolo kterého se otáčí otočné rameno – alhidáda. Spolu s alhidádou se okolo tohoto čepu otáčí i otočné zrcátko Z1 (indexové zrcátko).
Paprsek jdoucí od horizontu prochází nalevo od zrcátka Z2 přímo do dalekohledu. Paprsek jdoucí od objektu (např. Slunce nebo hvězdy) se odráží od zrcátka Z1 a poté od zrcátka Z2 a dopadá rovněž do dalekohledu. Při pohledu do dalekohledu sextantu uvidíme zorné pole svisle rozdělené na dvě poloviny. V levé polovině vidíme přímý obraz horizontu, v pravé polovině vidíme odraz oblohy. Sextant ukazuje úhlovou výšku objektu v okamžiku, kdy se nám podaří otáčením alhidády dostat objekt i horizont v zorném poli do koincidence (na jednu úroveň).
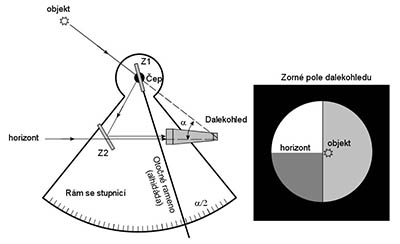 Geometrie odrazu od zrcátek způsobuje, že úhel natočení alhidády (tj. úhel, který svírají vůči sobě roviny zrcátek Z1 a Z2) je roven polovině úhlové vzdálenosti objektu od horizontu. Stupnice sextantu je ale konstruována tak, že na ní čteme přímo úhlovou vzdálenost. Vytíná-li tedy rám a stupnice sextantu šestinu kruhu (tj. 60°), lze sextantem měřit úhlové vzdálenosti až do 120°.
Geometrie odrazu od zrcátek způsobuje, že úhel natočení alhidády (tj. úhel, který svírají vůči sobě roviny zrcátek Z1 a Z2) je roven polovině úhlové vzdálenosti objektu od horizontu. Stupnice sextantu je ale konstruována tak, že na ní čteme přímo úhlovou vzdálenost. Vytíná-li tedy rám a stupnice sextantu šestinu kruhu (tj. 60°), lze sextantem měřit úhlové vzdálenosti až do 120°.
Sklon obou zrcátek u všech běžných sextantů je možné seřídit pomocí stavěcích šroubků, což (kromě vlastností získaných při výrobě) činí ze sextantu velice přesný přístroj (nejlevnější dostupný sextant, Davis Mk 3, má přesnost měření úhlů 1 – 2 úhlové minuty, profesionální sextanty mají přesnost desetkrát vyšší). Aby sextant ukazoval správně, musí být splněny dva předpoklady: (i) obě zrcátka musí být kolmá k rovině rámu, (ii) ukazuje-li alhidáda přesně 0°, musejí být obě zrcátka vzájemně rovnoběžná.
 Před každým měřením je tedy třeba věnovat péči seřízení zrcátek. Nejprve seřídíme kolmost indexového zrcátka (Z1), které má pouze jeden šroub. Položíme sextant indexovým zrcátkem k sobě a otočíme alhidádu tak, abychom viděli část stupnice sextantu a zároveň druhou část stupnice odrážející se v zrcátku (viz obrázek). Otáčením šroubu docílíme toho, aby okraj stupnice pozorovaný přímo napravo od zrcátka vytvářel s odrazem stupnice v zrcátku jedinou přímou linii.
Před každým měřením je tedy třeba věnovat péči seřízení zrcátek. Nejprve seřídíme kolmost indexového zrcátka (Z1), které má pouze jeden šroub. Položíme sextant indexovým zrcátkem k sobě a otočíme alhidádu tak, abychom viděli část stupnice sextantu a zároveň druhou část stupnice odrážející se v zrcátku (viz obrázek). Otáčením šroubu docílíme toho, aby okraj stupnice pozorovaný přímo napravo od zrcátka vytvářel s odrazem stupnice v zrcátku jedinou přímou linii.
Následuje seřízení horizontového zrcátka (Z2). Na to existuje několik různých postupů, popíšeme si pro začátečníka metodu nejsnazší – seřízení na sluneční kotouč. Před seřizováním (stejně jako před měřením) nejprve sklopíme sluneční filtry, kterými je sextant také vybaven, abychom si nepoškodili zrak. Alhidádu nastavíme přesně na 0° a podíváme se dalekohledem/průzorem sextantu na Slunce tak, aby hrana mezi skleněnou a odraznou částí zrcátka půlila sluneční kotouč. Při správně seřízeném zrcátku uvidíme jediný kotouček. Pokud je kotouček Slunce rozdvojený (ať již v horizontálním či vertikálním směru), musíme tyto dva obrazy spojit v jeden otáčením seřizovacími šrouby na zadní straně zrcátka. Jeden ze šroubů vždy posouvá obrazy vůči sobě horizontálně, druhý vertikálně.
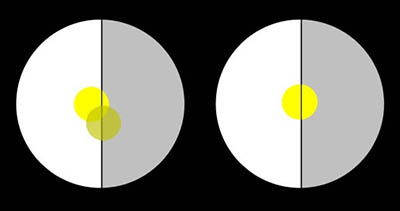 Jak již bylo řečeno, sextant slouží především k měření úhlové výšky těles nad horizontem. Na moři nám s výhodou poslouží mořský horizont. Při měření začínáme tím, že nastavíme sextant přibližně na 0° a namíříme jej na objekt na obloze (jako bychom hledali objekt v obyčejném dalekohledu). Po nalezení objektu jej v zorném poli umístíme do pravé části, abychom jej viděli pouze v zrcátku (nikoliv ve skle). Poté pohybem alhidády zvyšujeme úhel a zároveň sklápěním sextantu udržujeme měřený objekt v pravé části zorného pole. Následně uvidíme v levé části zorného pole (ve skle) mořský horizont. Objekt s horizontem uvedeme do přesné koincidence a na stupnici přečteme výšku objektu.
Jak již bylo řečeno, sextant slouží především k měření úhlové výšky těles nad horizontem. Na moři nám s výhodou poslouží mořský horizont. Při měření začínáme tím, že nastavíme sextant přibližně na 0° a namíříme jej na objekt na obloze (jako bychom hledali objekt v obyčejném dalekohledu). Po nalezení objektu jej v zorném poli umístíme do pravé části, abychom jej viděli pouze v zrcátku (nikoliv ve skle). Poté pohybem alhidády zvyšujeme úhel a zároveň sklápěním sextantu udržujeme měřený objekt v pravé části zorného pole. Následně uvidíme v levé části zorného pole (ve skle) mořský horizont. Objekt s horizontem uvedeme do přesné koincidence a na stupnici přečteme výšku objektu.
K tomu, abychom pomocí sextantu změřili skutečně nejkratší vzdálenost objektu od horizontu, museli bychom jej držet přesně ve svislé poloze, čehož lze dosáhnout jen obtížně. Pokud sextant není svisle, změřená vzdálenost bude vždy větší, než by měla být. Toho lze ale využít – kýváním sextantem ze strany na stranu, okolo osy dalekohledu, se objekt v zorném poli vzdaluje a opět přibližuje k horizontu. Správná – nejmenší úhlová výška objektu je pak v dolní úvrati tohoto obloučku.
Pozemský horizont k měření výšek objektů použít nelze, protože jeho výška je v každém azimutu jiná. Na souši se proto používá tzv. umělý horizont, což je nádoba naplněná kapalinou, jejíž hladina slouží jako ideálně vodorovné zrcadlo. Sextantem pak měříme úhlovou vzdálenost objektu na obloze od jeho odrazu v hladině. Díky jednoduché geometrii (zákonu odrazu) je tento změřený úhel roven přesně dvojnásobku výšky objektu nad ideální horizontální rovinou.
Aby bylo možné s naměřenými výškami objektů dále pracovat, je třeba je nejprve opravit o různé faktory, které naměřenou výšku ovlivňují. Jsou to zejména: – deprese horizontu (viditelný mořský horizont je níže než ideální), – refrakce (lom světla v atmosféře), – semidiameter (poloměr plošných objektů, jako Slunce nebo Měsíce) a v případě měření Měsíce ještě paralaxa (vliv malé vzdálenosti Měsíce od Země). Podrobný rozbor těchto oprav je mimo rámec tohoto článku. Čtenář nalezne jejich hodnoty např. v tabulkách určených pro navigaci – v Námořním almanachu.
Dostupné sextanty
Na (nejen) internetových aukcích lze dnes zakoupit velkou škálu sextantů, od různých levných atrap až po sběratelské historické exempláře. Pokud ale chceme pořídit nový sextant a používat ho k měření, lze doporučit nějakého českého prodejce a vybírat můžeme především z těchto tří variant:
Davis Mk 3
je jednoduchý plastový sextant, jehož cena se pohybuje okolo 1 800 Kč. Není vybaven dalekohledem, ale pouze průzorem, nemá ani mikrometrický bubínek. Jeho přesnost je od jedné do několika úhlových minut, takže polohu pomocí něj určíme s přesností na jednu až několik námořních mil.
Davis Mk 15
je plnohodnotný, ačkoliv také plastový sextant, jehož cena se pohybuje okolo 6 000 Kč. Jeho součástí je dalekohled, a také šnekový převod pro otáčení alhidády s mikrometrickým bubínkem. Ten umožňuje odečet hodnoty s přesností na 0,1 – 0,2 úhlové minuty (což je ale přesnost, které díky dalším vlivům dosáhneme jen málokdy; v praxi by ale chyba měření s tímto sextantem za ideálních podmínek neměla překročit 1 úhlovou minutu). Pro většinu aplikací je naprosto vyhovující. (Existuje i jeho vylepšená verze – Davis Mk 25. Je z odolnějšího plastu a jeho hlavním rozdílem oproti Davis Mk 15 je horizontové zrcátko, které není půlené, ale polopropustné v celé ploše. Horizont tedy vidíme přes celou šířku zorného pole, a rovněž Slunce nemusíme udržovat v pravé polovině. To je sice pro začátečníka mírnou výhodou, ale v polopropustném zrcátku téměř neuvidíme hvězdy, proto koupi této verze lze spíše nedoporučit).
Astra III B
je profesionální kovový sextant, dodávaný ve dřevěném kufříku. Jeho cena je okolo 13 000 Kč. Umožňuje odečet úhlů s přesností na 0,1 – 0,2 úhlové minuty a na rozdíl od plastových sextantů této přesnosti může zkušený uživatel skutečně dosáhnout. Má výbornou teplotní stabilitu.
Principy astronavigace
Jak ze změřených výšek objektů získáme naši polohu? Na to existuje mnoho různých metod, ale nejpoužívanější jsou dvě – metoda kulminace Slunce a metoda Interceptu, a ty si také popíšeme. Než se však pustíme do určování polohy, je třeba zdůraznit, že samotný sextant nám k určení polohy stačit nebude. K tomu je třeba mít k dispozici ještě přesný čas a také tabulky poloh objektů na obloze – Námořní almanach. Ten dnes může nahradit vhodný software, případně webová služba (viz odkazy na konci článku). K astronavigaci lze užít měření výšek Slunce, Měsíce, planet Venuše, Marsu, Jupiteru a Saturnu a dále některé z 57 navigačních hvězd, což jsou jasné hvězdy vybrané tak, aby pokud možno rovnoměrně pokrývaly celou nebeskou sféru. Před popisem zmiňovaných metod si také musíme definovat důležitý pojem – substelární bod (v případě Slunce jej označujeme jako bod subsolární, v případě Měsíce jako sublunární). Je to místo na povrchu Země, které se nachází přímo pod objektem (hvězdou). Pokud bychom se v tomto místě nacházeli, uvidíme daný objekt přímo nad hlavou. Zeměpisné souřadnice tohoto bodu označujeme jako GHA (greenwichský hodinový úhel), což je de-facto zeměpisná délka subsolárního bodu, a deklinace (Dec), což je jeho zeměpisná šířka. GHA a deklinace objektů používaných v navigaci, pro libovolné datum a čas v daném roce, tvoří hlavní náplň Námořního almanachu.
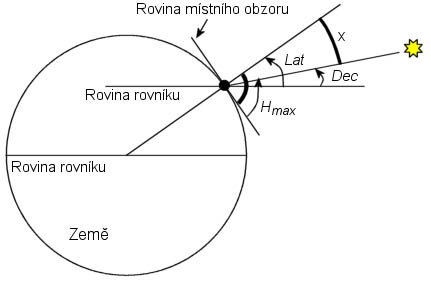 Metoda kulminace Slunce, nazývaná též metodou pravého poledne, spočívá v určení maximální výšky nad horizontem (Hmax), které Slunce dosáhne v průběhu své denní dráhy na obloze, a času, v němž k této maximální výšce, tzv. kulminaci, dojde. Z těchto dvou údajů získáme naše zeměpisné souřadnice následovně: v almanachu (softwaru) nalezneme pro dané datum a zjištěný čas kulminace GHA Slunce. Protože v okamžiku kulminace je Slunce přesně na jih od nás (pro jednoduchost předpokládejme měření z ČR nebo podobných šířek), leží také jeho subsolární bod na jih od nás; naše poloha i poloha subsolárního bodu jsou obě na společném poledníku. Nalezené GHA Slunce je tedy naší zeměpisnou délkou. V almanachu dále najdeme deklinaci Slunce, a z ní a výšky Hmax spočteme naši zeměpisnou šířku (Lat) pomocí vzorečku
Metoda kulminace Slunce, nazývaná též metodou pravého poledne, spočívá v určení maximální výšky nad horizontem (Hmax), které Slunce dosáhne v průběhu své denní dráhy na obloze, a času, v němž k této maximální výšce, tzv. kulminaci, dojde. Z těchto dvou údajů získáme naše zeměpisné souřadnice následovně: v almanachu (softwaru) nalezneme pro dané datum a zjištěný čas kulminace GHA Slunce. Protože v okamžiku kulminace je Slunce přesně na jih od nás (pro jednoduchost předpokládejme měření z ČR nebo podobných šířek), leží také jeho subsolární bod na jih od nás; naše poloha i poloha subsolárního bodu jsou obě na společném poledníku. Nalezené GHA Slunce je tedy naší zeměpisnou délkou. V almanachu dále najdeme deklinaci Slunce, a z ní a výšky Hmax spočteme naši zeměpisnou šířku (Lat) pomocí vzorečku
Lat = 90° – Hmax + Dec.
Odvození tohoto vzorečku objasňuje obrázek.
Pro metodu Interceptu měříme výšky minimálně dvou objektů, na rozdíl od předchozí metody ale nemusí být tyto výšky maximální. Začněme v popisu prvním z objektů, pro který jsme v čase T1 naměřili výšku nad obzorem H1. Pro čas T1 nalezneme v almanachu souřadnice substelárního bodu objektu (GHA, Dec), které jsou, jak již jsme uvedli, jeho zeměpisnými souřadnicemi. Protože substelární bod leží na povrchu Země přímo pod objektem, pokud bychom se nacházeli přímo v tomto bodě, objekt by se nacházel přímo nad naší hlavou. Jeho výška nad obzorem by tedy byla 90°. My jsme ale změřili výšku jinou: H1. Naše úhlová vzdálenost od substelárního bodu na povrchu Země je tedy 90° – H1. Všechna místa na povrchu Země s touto vzdáleností leží na kružnici se středem v substelárním bodě. Tuto kružnici nazýváme poziční kružnicí a někde na ní je naše poloha. Obdobně provedeme měření výšky H2 pro druhý objekt. Získáme tak druhou poziční kružnici se středem v substelárním bodě druhého objektu a poloměrem 90° – H2. Naše poloha je pak na průsečíku těchto dvou kružnic.
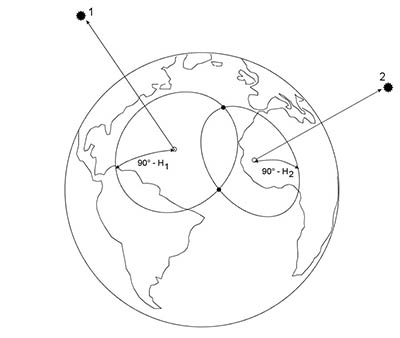 Tím jsme popsali základní princip metody Interceptu, v praxi se ale v této podobě nepoužívá z několika důvodů: 1. Poziční kružnice bychom mohli kreslit na zemském glóbu, ale ten má tak malé měřítko, že výsledný průsečík bychom získali pouze s velmi malou přesností. 2. Na mapě kreslit poziční kružnice nelze, protože mapové zobrazení nezachovává délky a kružnice se na mapě zobrazí jako složitější křivky. Navíc poloměry kružnic jsou obrovské a jejich středy budou většinou ležet mimo mapu, takže by ani nebylo kam „zapíchnout kružítko“. Tyto nesnáze se řeší tak, že namísto pozičních kružnic se do mapy kreslí jejich tečny – tzv. poziční přímky. Vzhledem k velkým poloměrům je nahrazení kružnic jejich tečnami velmi dobrou aproximací. Tečny se konstruují poblíž průsečíku obou kružnic, který ale dopředu neznáme, proto je základním předpokladem pro metodu Interceptu alespoň přibližná znalost naší polohy (tzv. poloha předpokládaná). Podrobný popis nalezení pozičních linií, které se řeší pomocí vzorců ze sférické trigonometrie (buď výpočtem, nebo pomocí tabulek či softwaru), by ale bylo nad rámec tohoto článku a zvídavého čtenáře odkážeme na zdroje k dalšímu studiu uvedené na konci článku.
Tím jsme popsali základní princip metody Interceptu, v praxi se ale v této podobě nepoužívá z několika důvodů: 1. Poziční kružnice bychom mohli kreslit na zemském glóbu, ale ten má tak malé měřítko, že výsledný průsečík bychom získali pouze s velmi malou přesností. 2. Na mapě kreslit poziční kružnice nelze, protože mapové zobrazení nezachovává délky a kružnice se na mapě zobrazí jako složitější křivky. Navíc poloměry kružnic jsou obrovské a jejich středy budou většinou ležet mimo mapu, takže by ani nebylo kam „zapíchnout kružítko“. Tyto nesnáze se řeší tak, že namísto pozičních kružnic se do mapy kreslí jejich tečny – tzv. poziční přímky. Vzhledem k velkým poloměrům je nahrazení kružnic jejich tečnami velmi dobrou aproximací. Tečny se konstruují poblíž průsečíku obou kružnic, který ale dopředu neznáme, proto je základním předpokladem pro metodu Interceptu alespoň přibližná znalost naší polohy (tzv. poloha předpokládaná). Podrobný popis nalezení pozičních linií, které se řeší pomocí vzorců ze sférické trigonometrie (buď výpočtem, nebo pomocí tabulek či softwaru), by ale bylo nad rámec tohoto článku a zvídavého čtenáře odkážeme na zdroje k dalšímu studiu uvedené na konci článku.
Další způsoby použití sextantu
Sextant jako přesný úhloměrný přístroj má i řadu dalších použití, především v tzv. terestrické navigaci, což je navigace v příbřežních vodách za použití útvarů, které vidíme na pevnině. Prvním z nich je určení vzdálenosti od objektu, jehož výšku známe. Takovým objektem může být například maják, jejichž výšky jsou uváděny v námořních mapách. Změříme úhlovou vzdálenost α mezi vrcholkem majáku a jeho patou (přesněji mezi místem, kde je umístěno jeho světlo, a mořským břehem, protože výšky v mapách udávají výšku světla nad mořskou hladinou) a získáme naši vzdálenost od paty majáku jako
D = H / tan(α),
kde H je výška majáku (D i H budou ve stejných jednotkách). Protože pro malé úhly platí, že tangens úhlu je přibližně roven hodnotě úhlu v radiánech, lze přepsat vzoreček do nejčastěji užívané podoby:
D = 1,856 H / α,
přičemž H dosazujeme v metrech, α v úhlových minutách a D vyjde v námořních mílích.
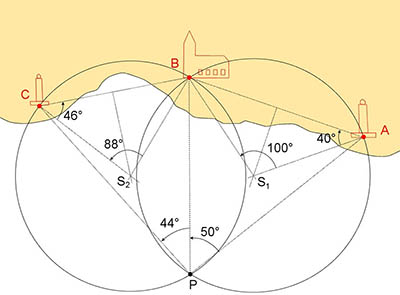
Při druhém způsobu použití sextantu při terestrické navigaci měříme horizontální úhly mezi objekty na pobřeží (jejich polohu opět musíme identifikovat na mapě). Protože sextantem měříme úhly velice přesně, je tato metoda mnohem přesnější, než například konstrukce pozičních linií k identifikovaným bodům na pobřeží na základě azimutu změřeného náměrovým kompasem. V případě měření sextantem potřebujeme ale k určení polohy alespoň tři body. Změřením horizontálního úhlu mezi dvěma body, např. mezi majákem A a kostelem B na obrázku, získáme na mapě poziční kružnici ABP. Platí totiž, že úhel APB pro libovolný bod P ležící na kružnici je roven polovině úhlu AS1B, kde S1 je středem této kružnice. Po zaměření úhlu mezi dvěma objekty A a B (v našem příkladu 50°) tedy postupujeme takto: sestrojíme osu úsečky AB a dále z vrcholu A vedeme polopřímku, svírající s úsečkou AB úhel rovný doplňku změřeného úhlu APB do 90° (tedy 40°). V průsečíku osy úsečky a této polopřímky leží střed hledané kružnice (S1). Okolo tohoto středu opíšeme kružnici ABP a získáme poziční kružnici. Analogicky postupujeme v případě druhého horizontálního úhlu, změřeného mezi objekty B a C (v našem příkladu 44°). Získáme druhou poziční kružnici a v jejich průsečíku je naše poloha – bod P.
Postup vynesení pozice ze dvou horizontálních úhlů lze usnadnit a urychlit pomocí přístroje označovaného jako tříramenný úhloměr (three-angle protractor, nebo též station pointer). Ramena přístroje se nastaví tak, aby vzájemně svírala oba změřené úhly, a přístroj se položí na mapu do takové polohy, aby hrany ramen procházely pozicemi měřených objektů. Uprostřed stupnice přístroje je malý otvor, v němž se pak nachází naše poloha. Před nástupem GPS byl kovový station pointer běžnou navigační pomůckou na lodích, dnes se stává už spíše sběratelským artiklem, lze ale sehnat jeho plastovou variantu.
Zdroje k dalšímu studiu:
- Petr Scheirich: Základy astronavigace pro začátečníky.
- Navigator Light freeware – software pro zpracování základních astronavigačních měření a určení polohy: http://www.tecepe.com.br/nav/download.htm
- Online Nautical Almanac
-
Webová služba vhodná pro snadné zpracování měření metodou interceptu: http://aa.usno.navy.mil/data/docs/celnavtable.php
Autor: Mgr. Petr Scheirich, Ph.D., Astronomický ústav AV ČR, v. v. i.
levotočivé úhly
děkuji za pěkný článek, rád bych se jen optal, zda se při námořní navigaci užívají "levé" úhly?
u pozemní geodezie se užívají pravé. na výpočet to ve vašem případě (předposlední obrázek) samozřejmě nemá žádný vliv, jen by mě to zajímaloRe: levotočivé úhly
Dobrý den,
když se teď dívám na předposlední obrázek, skutečně jsou tam šipky vyznačené tak, jako by úhly stoupaly zprava doleva (tj. "levé" úhly). Když jsem obrázek vytvářel, nakreslil jsem šipky jak mě právě napadlo a nad jejich orientací nepřemýšlel, protože, jak píšete, na výsledek to nemá vliv.
Jinak při samotném měření (pomocí sextantu) se používají úhly stupající zleva doprava a to čistě z praktických důvodů: sextant se při tomto měření drží vodorovně a je jednodušší jej držet rukojetí obrácenou dolů. V této poloze se pak úhel na sextantu zvětšuje od objektu levého (který je na nule) směrem k objektu pravému. Dalo by se to dělat i opačně, jen by to bylo méně pohodlné. Nesetkal jsem se ale ani v praxi, ani v teorii námořní navigace, že by byl nějaký úzus na to, která varianta je ta "správná".
Při vynášení do mapy pomocí tříramenného úhloměru (poslední obrázek) se pak používají úhly "levé" i "pravé", protože úhel levého ramene narůstá směrem doleva a úhel pravého ramene narůstá doprava. Vzhledem k tomu, že úhly jsou při tomto měření vždy kladné a také vždy menší než 180° (sextant ani nic jiného měřit neumožňuje, s výjimkou velice malých záporných úhlů), nehrozí zmatky při záměně levé/pravé strany.
V námořní navigaci ale existuje ještě jedna metoda určení polohy - pomocí náměrového kompasu (té se ovšem tento článek nevěnuje), kdy určujeme azimuty k význačným bodům nebo majákům na pobřeží a ty pak vynášíme do mapy. Protože azimut kompasu může být od 0 do 360, tak v tomto případě se zásadně používají (jak při měření, tak při vynášení) pouze úhly narůstající směrem doprava.
S pozdravem,
Petr Scheirich
kulminace vs. prave poledne
Vazeny Mgr.et Ph.D,
v pripade Slunce neni cas pravehio poledne(pruchodu polednikem) roven casu kulminace. Vite proc?
Salve J.L.Re: kulminace vs. prave poledne
Dobry den,
ano vim, a tesi me, ze jste si tohoto zjednoduseni v clanku vsiml. Je to dano (i v pripade, ze se meri z pevneho stanoviste) zmenou deklinace Slunce v prubehu dne.
Vice k tomuto vlivu a jak ho opravit lze nalezt napr. v odkazovane publikaci Zaklady astronomie pro zacatecniky:
(http://sajri.astronomy.cz/astronavigace/zaklady_astronavigace.pdf) kap. 8.3
S pozdravem,
Petr Scheirich